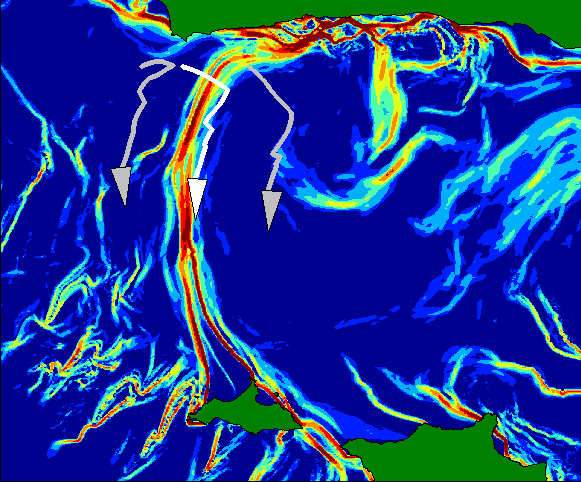
Distributed Sensing and Tracking of Geophysical Flows

Posted on by

Geophysical fluid dynamics (GFD) is the study of natural large-scale fluid flows, such as oceans, the atmosphere, and rivers. GFD flows are naturally stochastic and aperiodic, yet exhibit coherent structure. Coherent structures are important because they enable the estimation of the underlying geophysical fluid dynamics.   While these transport controlling structures in GFD flows are inherently complicated and unsteady, their understanding is necessary for the design of robust underwater vehicle control and the prediction of various physical, chemical, and biological processes that in GFD flows.  Nevertheless, the data sets that describe GFD flows are often finite-time and of low resolution and most transport controlling features in fluids are unstable and non-stationary, this renders the problem of “mapping” these features using teams of autonomous vehicles highly challenging.

The goals of this project are to overcome the theoretical and technical challenges and develop a general mathematical and control framework for distributed autonomous sensing and tracking of geophysical fluid dynamics in 2D space over time (2D+1) and in 3D space over time (3D+1).  The key idea exploits the capability of the team to cover large regions in physical space to increase the spatio-temporal sampling resolution of the flow field. The data will then be processed in a distributed fashion by the team to obtain a global description of the flow dynamics that can be maintained and updated in real time.  Objectives of this work include:

  1. Identifying and evaluating key kinematic features that control transport in oceanic surface flows of greatest relevance to autonomous vehicle navigation and control;
  2. Synthesizing distributed sensing and tracking strategies for a class of transport controlling features in 2D, 2D+1, 3D, and 3D+1 flows;
  3. Developing a general mathematical and control framework for teams of autonomous vehicles that leverages key transport controlling features in oceanic flows for improved navigation and monitoring of dynamic and uncertain environments;
  4. Developing a new control and coordination framework that leverages the disparate sensing, mobility, and computational capabilities within a heterogeneous teams of mobile robots for ocean monitoring;
  5. Experimentally validate the proposed strategies via a proof-of-concept robotic system with simulated and realistic flow data.

Videos

Two Robots Straddling a Manifold in the Multi-Robot (MR) Tank



Two robots driving on opposite sides of the stable manifold of saddle point in an actual time-invariant flow created in the MR tank. The robots are obtaining measurements of the flow field using their onboard flow sensors which are capable of measuring both the speed and direction of the current relative to the robot’s movements. Global position for the robots are provided using an external OptiTrack motion capture system.

Tracking Lagrangian Coherent Structures



Three-robot manifold/LCS tracking strategy validated on a periodic wind-driven double-gyre model, experimental data, and actual ocean data.



Full simulation run three robots tracking the LCS off the coast of Santa Barbara, CA.

Papers

  1. D. Kularatne and M. A. Hsieh. “Tracking Attracting Manifolds in Flows,” Autonomous Robots, 41(8), Mar 2017, pp. 1575–1588. Bibtex | PDF
  2. M. Michini, M. Ani Hsieh, E. Forgoston, and I. B. Schwartz. “Robotic Tracking of Coherent Structures in Flows,” IEEE Trans. on Robotics, Vol. 30, No. 3, 593-603, Jun 2014. Bibtex | PDF
  3. D. Kularatne and M. A. Hsieh. “Tracking Attracting Lagrangian Coherent Structures in Flows,” in the 2015 Robotics: Science and Systems (RSS 2015), July 2015, Rome, Italy. BibTeX | PDF
  4. M. Michini, M. A. Hsieh, E. Forgoston, and I. B. Schwartz, “Experimental Validation of Robotic Manifold Tracking in Gyre-Like Flows,” in the IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS’14), Sep 2014, Chicago, IL USA. BibTeX | PDF
  5. M. Michini, H. Rastgoftar, M. A. Hsieh, and S. Jayasuriya, “Distributed Formation Control for Collaborative Tracking of Manifolds in Flows,” in the 2014 American Control Conference (ACC 2014), Jun 2014, Portland, Oregon USA. BibTeX | PDF
Posted in past-projects.