The central focus of this work is to extract predictive models of complex, nonlinear dynamical systems from data. We focus on strategies that enable feature-based representations of complex spatiotemporal processes and techniques that can embed expert and prior physical knowledge. Our aim is to extract model representations that are amenable for planning, control, and uncertainty quantification. In addition, we aim to develop techniques that gives new physical insights into the complexities of physical, chemical, and biological processes in natural environments like the ocean, atmosphere, and rivers.
KNODE
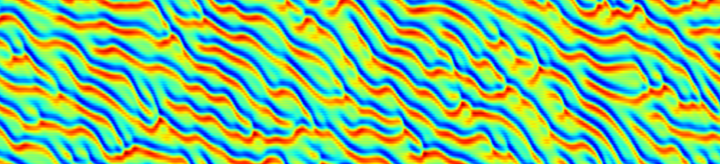
Knowledge-based Neural Ordinary Differential Equations (KNODE) is a universal machine learning framework that can extract predictive models for nonlinear systems based on observation data. KNODE has the ability to model general classes of dynamical systems and reconcile data-driven models and first principles knowledge. KNODE has been shown to work for systems with nonlinear and chaotic dynamics, high-dimensional systems, and KNODE models have been successfully used with model predictive control.
Learning Transfer Operators
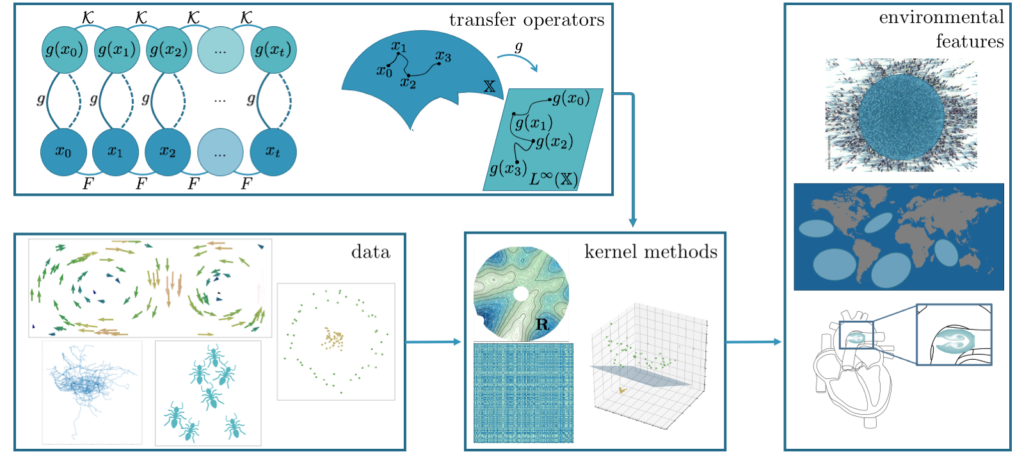
Transfer operators are powerful tools used to represent the global dynamics of complex spatiotemporal systems. Ascertaining global dynamics from noisy, local sensor measurements collected by robots is challenging but fundamental to their success in monitoring or operating within these environments. This work focuses on developing machine learning strategies to represent transfer operators from data. The ability to understand global dynamics from data enables robots to identify persistent features and these features can be leveraged to improve decision making, planning, and control.
KNODE-MPC
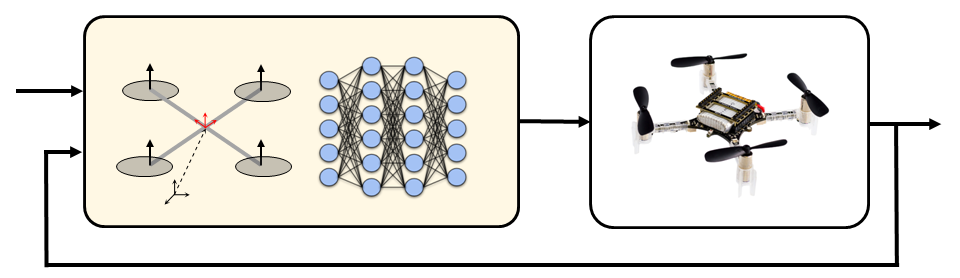
KNODE-MPC applies KNODE in a predictive control framework. This work uses KNODE to derive and incorporate accurate dynamic models for model predictive control (MPC). MPC relies on precise dynamic models to achieve the desired closed-loop performance. However, the presence of uncertainties in complex systems and the environments they operate in pose a challenge in obtaining sufficiently accurate representations of the system dynamics. In this framework, KNODE is used to augment a model obtained from first principles. The resulting hybrid model encompasses both a nominal first-principle model and a neural network learnt from simulated or real-world experimental data. By applying this framework to a quadrotor system, KNODE-MPC shows that the hybrid model provides more accurate predictions of the system dynamics and is able to generalize beyond the training data. Furthermore, experimental results show that the integrated KNODE-MPC framework achieves improved closed-loop trajectory tracking performance.
Relevant Papers
- T. Salam and M. A. Hsieh. “Heterogeneous robot teams for modeling and prediction of multiscale environmental processes,” submitted to Autonomous Robots, Under Review, on arXiv https://arxiv.org/pdf/2103.10383.pdf.
- T. Z. Jiahao, L. Pan, and M. A. Hsieh. “Learning to Swarm with Knowledge-Based Neural Ordinary Differential Equations,” accepted to IEEE International Conference on Robotics and Automation (ICRA2022), May 2022, Philadelphia, PA USA, https://arxiv.org/pdf/2109.04927.
- K. Y. Chee, T. Z. Jiahao and M. A. Hsieh. “KNODE-MPC: A Knowledge-Based Data-Driven Predictive Control Framework for Aerial Robots,” in IEEE Robotics and Automation Letters, vol. 7, no. 2, pp. 2819-2826, Apr 2022, 10.1109/LRA.2022.3144787.
- T. Salam, V. Edwards, and M. A. Hsieh. “Learning and Leveraging Features in Flow-Like Environments to Improve Situational Awareness,” in IEEE Robotics and Automation Letters, vol. 7, no. 2, pp. 2071-2078, Apr 2022, 10.1109/LRA.2022.3141762.
- T. Z. Jiahao, M. A. Hsieh, and E. Forgoston. “Knowledge-based learning of nonlinear dynamics and chaos,” in Chaos 31(11), Nov 2021, https://doi.org/10.1063/5.0065617.
- M. Qraitem, D. Kularatne, E. Forgoston, and M. A. Hsieh. “Bridging the Gap: Machine Learning to Resolve Improperly Modeled Dynamics,” in Physica D: Nonlinear Phenomena, 414, 132736 (Dec 2020), https://doi.org/10.1016/j.physd.2020.132736.
Acknowledgements
To come …