Path Planning

Posted on by

Optimal Paths in Flows

Snapshot of a visualization of ocean surface currents for June 2006 through December 2007, generated using data compiled by the NASA Estimating the Circulation and Climate of the Ocean (ECCO) project. Image courtesy of NASA/Goddard Space Flight Center Scientific Visualization Studio https://svs.gsfc.nasa.gov/

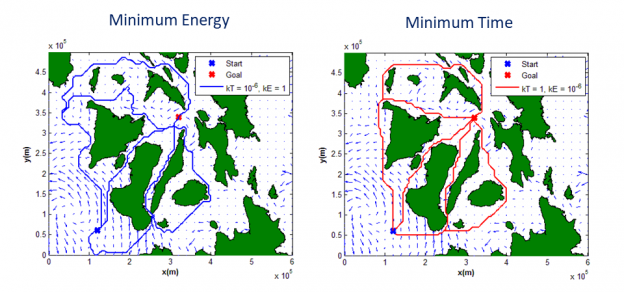
Autonomous marine vehicles (AMVs) are typically deployed for long periods of time in the ocean to monitor different physical, chemical, and biological processes. Given their limited energy budgets, it makes sense to consider motion plans that leverage the dynamics of the surrounding flow field so as to minimize energy usage for these vehicles.  This project focuses on developing suitable graph search based techniques to compute energy and/or time optimal paths for AMVs in two- and three-dimensional time-varying flows (2D+1 and 3D+1).   This project has contributed novel techniques that can capture the kinematic actuation constraints on the vehicles in our cost functions, generate optimal paths in different homotopy classes, and employ an adaptive discretization scheme to construct the search graph.  Our current efforts are focused on how best to leverage coherent structure information into our strategies.

This work is a collaboration between Dr. Subhrajit Bhattacharya at Lehigh University.

Papers

  1. D. Kularatne, M. A. Hsieh, and E. Forgoston.  “Using Control to Shape Stochastic Escape and Switching Dynamics,” Chaos 29, 053128 (2019); https://doi.org/10.1063/1.5090113.  Bibtex | PDF
  2. D. Kularatne, S. Bhattacharya, and M. A. Hsieh. “Going With The Flow: A Graph Based Approach to Optimal Path Planning in General Flows,” Autonomous Robots: RSS 2016 Special Issue, 42(7), Oct 2018, pp 1369 — 1387. Bibtex | PDF
  3. D. Kularatne, E. Forgoston, and M. A. Hsieh. “Exploiting Stochasticity for Navigation in Gyre Flows,” in the Proc. of the 2018 Robotics: Science and Systems (RSS 2018), Jun 2018, Pittsburgh, PA USA. Bibtex | PDF
  4. H. Hajieghrary, D. Kularatne, and M. A. Hsieh. “Differential Geometric Approach to Trajectory Planning: Cooperative Transport by a Team of Autonomous Marine Vehicles,” in the Proc. of the 2018 IEEE American Control Conference, Jun 2018, Milwaukee, WI USA. Bibtex | PDF
  5. D. Kularatne, H. Hajieghrary, and M. A. Hsieh. “Optimal Path Planning in Time-Varying Flows with Forecasting Uncertainties,” in the Proc. of the 2018 IEEE International Conference on Robotics and Automation (ICRA2018), May 2018, Brisbane, Australia. Bibtex | PDF
  6. D. Kularatne, S. Bhattacharya, and M. A. Hsieh. “Optimal Path Planning in Time-Varying Flows using Adaptive Discretization,” IEEE Robotics and Automation Letters (RA-L), 3(1), Jan 2018, pp. 458-465.  Bibtex | PDF
  7. D. Kularatne and M. A. Hsieh. “Tracking Attracting Manifolds in Flows,” Autonomous Robots, 41(8), Mar 2017, pp. 1575–1588. Bibtex | PDF
  8. D. Kularatne, S. Bhattacharya, M. A. Hsieh. “Time and Energy Optimal Path Planning on a Flow Field,” in the Proc. of the 2016 Robotics: Science and Systems (RSS2016), Jun 2016, Ann Arbor, MI USA. Bibtex | PDF

Path Planning for a Magnetic Millirobot

For actuation of small-scale robotic systems, magnetic control methods have garnered significant interest since magnetic fields can be selectively applied without affecting non-magnetic materials. Existing approaches for the control of single or multiple microrobots operating in magnetic fields have mostly focused on two aspects of the problem: 1) design of the physical geometry of the robot, and 2) design of devices to manipulate the local magnetic field. Instead of focusing on ways of manipulating the local magnetic field or the physical geometry of the robot, this project investigates how global design of the field topology can be leveraged for control and manipulation of microrobots. A significant advantage of leveraging topological features of the force vector field is that it does not require complete knowledge of the field and yet results in comparable performance to vehicles following optimal paths where the vector field has been explicitly accounted for.

We create a path planning and trajectory following strategy for a magnetic millirobot that leverages the nonlinearities in the external magnetic force field (MFF). The strategy creates a library of candidate MFFs and characterizes their topologies by identifying the unstable manifolds in the workspace. The path planning problem is then posed as a graph search problem where the computed path consists of a sequence of unstable manifolds segments and their associated MFFs. By tracking the robot’s position and sequentially applying the MFFs, the robot navigates along each unstable manifold until it reaches the goal.

Videos

Papers

  1. A. Mansfield, D. Kularatne, E. Steager, and M. A. Hsieh, “A Topological Approach to Path Planning for a Magnetic Millirobot,” Submitted to Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS2020), Under Review, Oct 2020, Las Vegas, NV.

Posted in current-projects.